最近は、知財戦略について書いていますが、新型コロナウイルスで非常宣言事態が発出されるなど、緊迫した状況になってきました。そこで、日本の新型コロナウイルス対策について、 この対策で本当に大丈夫なのか、 門外漢でありますが、 少し調べてみました。
新型コロナウイルス対策について
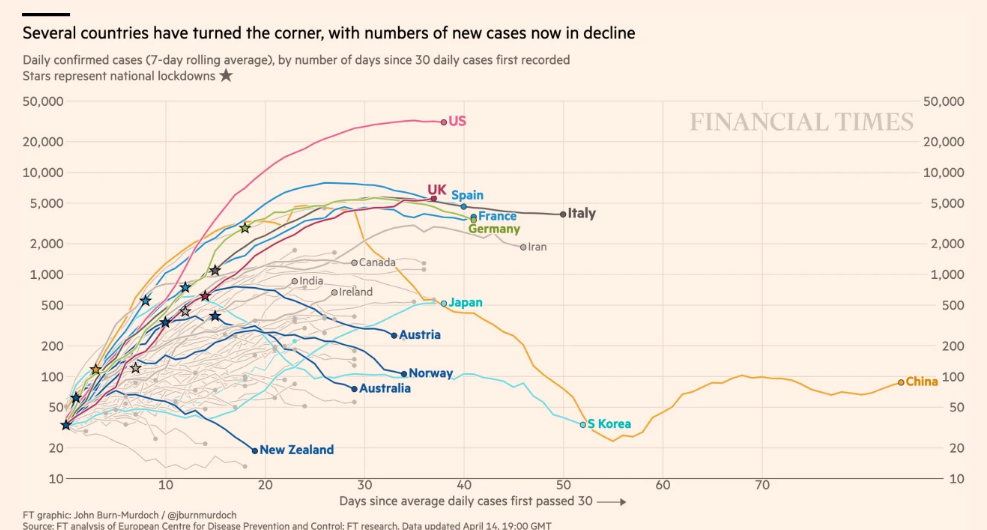
下図は、FINANCIL TIMESに掲載されている2020年4月14日の世界の新型コロナウイルスの新規感染者数の動向です。縦軸は、7日ローリングアべレージの新規感染者数で対数で表されており、横軸は新規感染者数が30人に達したときからの経過日数を表しています。
米国、イギリス、イタリア、ドイツ、スペインはようやく新規感染者数は頭を打って減少に転化し始めました。しかし、累積感染者数は、面積になりますので、新規加入者数が0になるまで増加し続けます。例えば、米国は現在新規感染者数は25,000人、累積感染者数が600,000人ですので、中国のようなパターンで減少したとしても、累積感染者数は増加し続け1月後に120万人程度になると予想されます。
各国の新規感染者数が減少に転じ始めている中、日本では、直線的(指数関数的)に新規加入者数が増加し始めて、非常に心配な様相を呈しし始めています。
日本の新型コロナウイルス対策の戦略は問題はないか
新型コロナウイルスのような人から人へ感染する感染症の場合の封じ込めの基本戦略は感染者を二次感染が起らないようにできる限り早く隔離することです。
新型コロナウイルスですっかり信用を落としてしまったWHOのテドロス事務局長ですが、彼の「テスト、テスト、テスト」の発言は感染症対策の本質をついています。
この戦略を採って成功したのが、シンガポールと台湾です。日本でも、和歌山県が院内感染の発生時に、関係しそうな人すべてについてPCR検査を徹底的に行い封じ込めに成功しました。
しかし、なぜか、クラスター対策班はその方向性として
・中国やシンガポールの対策とは異なる日本独自の対策の構築を目指す
・疫学解析・数理モデル解析により最適解を探っていく
として、壮大な実験を始めました。
その理由として、 SARSとCOVID-19の疫学的違いを挙げ
• SARS: ほとんどすべての感染者が重症化し、そのためにすべての感染連鎖を検出し、それらをすべて断ち切ることで封じ込め に成功した
• COVID-19: 多くの感染者が無症候・軽症であり、すべての感染連鎖を見つけることはほぼ不可能
だからとしています。
そして、 日本の対策の3本柱として
①クラスター(集団)の早期発見
②早期対応 •患者の早期診断、重症者への集中治療の充実と 医療提供体制の確保
③市民の行動変容
を掲げています。
そのとおりだと思いますが、しかし、感染症対策の基本である検査による感染者の早期発見・早期隔離の視点が抜け落ちています。
多分、①の対策でこれが実施できるとの考え方だと思われますが、①の対策だけでは、その網にかからない感染者が相当発生し次第に制御不能になってしまいます。
したがって、①は「感染者の早期発見」が主で、その一つの手段としてクラスター等を早期に発見し、感染者の経路追跡を実施するとすべきです。
加えて、日本の検査体制が貧弱で、あれだけ、テレビで岡田先生が、まずPCR検査をすべきとしていたにもかかわらず、なぜか多くのPCR検査ができていない現状があったことは否めないと思います。
PCR検査は、確度が低くやっても無駄だという人がいますが、現状、感染者の検出の唯一の方法であるならば、なによりもまずPCR検査体制を強化すべきです。
感染拡大のメカニズム
感染が拡大する要因について見て行きます。もっとも重要な概念は基本生産数 (basic reproduction number) というもので、 R0 という普遍的な記号で表されます。
基本再生産数 R0
R0 は、「 感染者が平均で何人にうつすか」ということを表します。少し厳密に東大の稲葉先生は「なんらかの病原体 (ウイルスや細菌など)に対してすべて が感受性(susceptible)を有する個体からなるホスト ( 宿 主)人口(個体群)集団において典型的な1人の感染者 が、その全感染期間において再生産する2次感染者の期待数 」とされています。
感染個体が単位時間あたり平均 β の感染を生み出す接触をし、感染期間の平均を τ としますと、 R0 は
\[R_0=β×τ\tag a\]
と表されます。
R0 は出生率と同様に、R0 > 1 のとき、感染が拡大し、R0 < 1 のときは感染が減少し、 R0 =1のときは、その状態を維持します。
新型コロナウイルスの場合は、 R0 をドイツで推定しているように、2.5とし、 感染期間の平均 τが30日程度としますと、βは0.083となります。
R0 が2.5であれば、なにもしなければ、感染が指数関数的に増加します。(どれぐらい増加するかは次の数理モデルの項で説明します。)
従って、感染を減少させるためには、何らかの制限pをして、実際の再生産数(実行再生産数\(R_e\))を1以下にする必要があります。そのためには、
\[R_e=(1-p) R_0<1\tag b\]
を満たすようにする必要があります。
したがって、R0 が2.5のときは、p>0.6、即ち6割以上の何らかの制限をする必要があることになります。
感染拡大を防止するための方策
上記に述べましたように、感染拡大を防止するには、実行再生産数 \(R_e\) を1以下にする必要があります。基本再生産数 R0 は何も対策を施さない場合のものでありますが、実行再生産数 \(R_e\) は対策を施したときの値で、 R0 と同様に
\[R_e=β×τ\tag c\]
と表せます。
従って、感染拡大を防止するための対策としては
① 単位時間あたりの感染を生み出す接触を表す平均 β を減らすこと
② 感染期間を表す平均 τ を減らすこと
です。
①は単位時間あたりの他者との接触を減らすことで、例えば、家に留まる(ステイホーム)やマスクなどの防護具を装着することなどで、この対策の究極にあるのが、まさに、現在、緊急事態宣言のもと日本で行っていることや、各国で行っているロックダウンです。
これには、膨大な費用と犠牲が伴い、経済が破綻するおそれさえあります。
②は、感染者をできるだけ早く発見し、隔離して感染の機会を除くことで、病院に入院することや死亡も含まれます。
新型コロナウイルスの場合、感染しても発症しなくて、その間に他者に感染させるので、早期発見して隔離するのが難しいケースがありますが、これには和歌山県が実施したように、関係者を根こそぎテストする方法をとればかなりの確率で隔離できる可能性があります。
また、プライバシーを配慮しながらグーグルとアップルで開発しようとしているようなアプリの利用も期待できます。
②の対策は①の対策に比べて、桁違いの小さなコストで実行できます。
数理モデルによる感染拡大メカニズム
クラスター対策班の方向性としての新型コロナウイルスの対策として、 「疫学解析・数理モデル解析により最適解を探っていく 」としています。
この数理モデルとはどのようなものでしょうか。基礎となる単純な数理モデルでよく知られているのとしては、SIR、SIS、SEIRなどのモデルがあるようです。
SIRモデルは、
\begin{eqnarray}
\frac{dS(t)}{dt)} & = & -βS(t)I(t)\tag{1}\\
\frac{dI(t)}{dt)} & = & βS(t)I(t)-γI(t)\tag{2}\\
\frac{dR(t)}{dt} & = & γI(t)\tag{3}
\end{eqnarray}
で表されます。
ここで、
・S(t)は感受性人口 (susceptibles:感 染する可能性のある人口)
・I(t)は 感染人口 (infectives: 感染していてかつ感染させる能力のある人口)
・R(t)は 隔離された人口 (recovered/removed:病気からの 回復による免疫保持者ないし隔離者・死亡者)
・β は感染率
・γ は隔離率
このモデルは、 βI(t) は 感染力 (force of infection) であり、単位時間あたり単位人口あたりの感受性人口感染率を表し、 感染力が感染人口サイズに比例しているものとし、その比例係数が β で、また感染した人は一定の率 γ で回復(死亡を含む)、ないし隔離(入院)されるという仮定を置いています。
今、初期段階においては感受性人口 S(t)に対して感染人口 I(t)は非常に少数なので、そのときに 全感受性人口のサイズを\(S_0\) といたしますと、S(t) はほとんど \(S_0\) に近いので、(2)式は
\[\frac{dI(t)}{dt} = (βS(0)-γ)I(t)\]
となり、\(λ_0 = (βS(0)-γ) \)とおくと、(2)式は数学的に簡単に解けて、流行初期においては感染者人口は I(t) は
\[I(t) = I(0)\mathrm{e}^{ λ_0 t}\]
となり、 \(λ_0 > 0\)ときに指数関数的に増加することが分かります。
この感染拡大条件を書き直せば
\[\frac{βS(0)}{γ} > 1\]
となります。
従って、これは、式(a)の 感染期間の平均 τ は
\[τ = \frac{γ}{βS(0)} \]
なので、上記した基本再生産数 R0 に相当しますので、
\[K_0 = β×τ = \frac{βS(0)}{γ} \]
と表されます。
SIRモデルは非常に単純なモデルですが、基本再生産数 で議論した R0 の値により感染者数I(t)がどのようになるかを数値的に理解できるようになります。
下図は\(R_0\)の値を変えた時の感染者数I(t)と回復数者R(t)を表したものです。
本来私が作成すべきですが時間がないので、神戸大学の牧野先生の図をそのまま拝借しています。詳細はこちらをご覧ください。
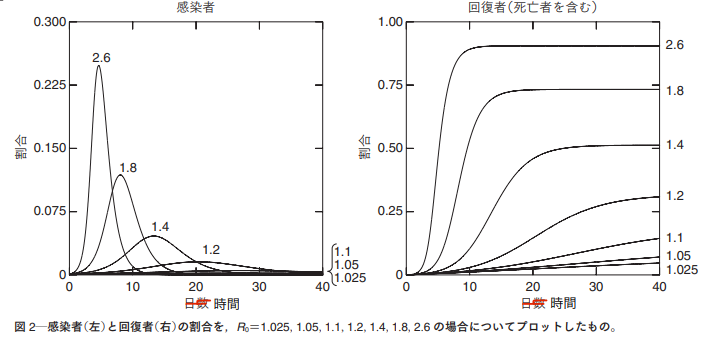
実行再生産数 \(R_e\) の値により、感染者数、死亡者数が大きく変化することが分かります。
人との接触を「8割削減せよ」との意味
緊急事態宣言のもと、人との接触の機会を8割削減することが、要請され、何で8割かの根拠に新聞に下記の図が示されています。
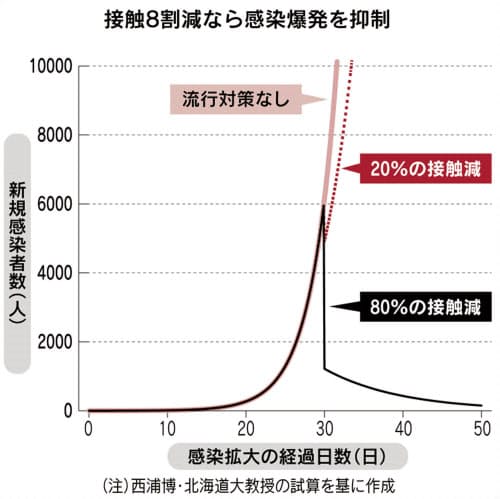
この図を見たとき率直にいって8割に接触を削減すれば、感染者数が垂直に減少するように描かれており、全く根拠が示されいなくて、眉唾ものではないかと思いました。
そこで、調べてみました。これも、神戸大学の牧野先生が「新型コロナウイルスに関するめも」で、解説されていました。
基本再生産数 R0 が2.5で推移させ、それで式(b)の制限pを0.2と0.8のケースを図にしたものとされています。ここでの縦軸は感染者数I(t)でなく新規感染者数\(I(t+⊿t)-I(t)\)であることに注意が必要です。
すなわち、
20%削減は\(R_e = (1-0.2)R_0\)なので実行再生産数は\(R_e=0.8R_0=2\)のグラフになります。
80%削減は\(R_e = (1-0.8)R_0\)なので実行再生産数は\(R_e=0.2R_0=0.5\)のグラフになります。
直線になるのは、\(R_e\)が2.5から0.5まで変わるためです。
ここでいっていることを正確に言うと、基本生産数 R0 を2.5とし、制限値pを0.8にしたとき実行再生産数 \(R_e\) が0.5になるということだけです。 したがって、人との接触を8割削減しても、\(R_0\)が0.5になるとは限りません。また、この議論は基本再生産数 R0 を基本に8割削減することを要請していますが、3月19日の専門委員会の資料では 実行再生産数\(R_e\) を1程度に推計していますので、これですとpを0.5とすれば、 \(R_e\) は0.2となりますので、5割の制限でよいことになります。
また、SIRモデルは1人から感染が拡大する単純なモデルです。しかし、数人の感染者かいるような複雑なモデルでは、制限pが実行再生数に与える影響が大きいとしている論文もあります。
現状のようなテストをしなくて、市中感染が発生している状況では、感染者の増加を抑えるには人との接触を断ち切る必要があることは否めませんが、テスト不足により、実質的なτが大きくなり、 実行再生産数 \(R_e\) が減少しない可能性もあり議論が乱暴すぎます。
行動制限しても、病院や介護施設、家庭などの人の滞留場所では、感染が蔓延します。 何にもましてテストをして、感染者を隔離するのが1番です。 しかし、感染がここまで蔓延すれば、強烈な接触制限を取らなければならないことも致し方ないことです。
予測モデルとリアルタイム・シュミュレーションシステムの開発
今最も望まれるのは難しい数学を使った数理モデルの数学的解析でなく、現状の状態を把握でき数週間から1月先の正確な感染者数の数値計算によるリアルタイム予測です。現在発表されているデータは8日前のデータです。実行再生産数が1より大きければ、感染者は指数関数的に増加しますので、8日間で何倍にも増加します。したがって、8日もの遅れは制御するのに致命的です。
既に、西浦先生など対策班でシステムを構築して、シュミュレーションを行い正確な感染者の予測をされていると思いますが、感染者をリアルタイムに予測し、また、制限値のパラメータを変更すればどうなるかなどの正確な推計値を得ることが、感染の制御には欠かせません。また、各地域の感染状況が見える化し、これにより国民に正確な情報を知らせ適切な行動をとってもらうことが不可欠です。
上にのべたような単なる数理モデルを使って、このまま何もしなければ、40万人が死亡するといった情報で国民を脅かすだけでは、十分な対策はとれません。
非常事態宣言の出口戦略
まず、今回の緊急事態宣言により、感染をコントロールできるレベルまで感染者数を下げることは必要不可欠です。
中国が武漢封鎖戦略をとっても、フィナンシャルタイムズの図にあるように50日程度を要しています。日本の場合これより緩やかな措置ですが、非常事態宣言時の実行再生産数は、かなり低いと考えられるので、30日から40日程度で1日あたりの感染者数が100以下にできることを信じています。
このままでは経済が持ちませんから、できるだけ早く経済を動かす必要があります。
そのためには、緊急事態宣言を解除して人が移動しても、感染を制御できるシステムを早急に構築する必要があります。
それには、できる限り多くのテストをして、感染者を早期発見し、徹底的に接触者の追跡をし、感染者の早期隔離を行うことです。そして、感染者、隔離施設、病院などの情報を集中一括管理することと感染者数のリアルタイム予想を行うシステムの構築することが不可欠です。
通常、経済活動をするには、海外からの感染の流入を考えると、おそらく感染者数を0にすることは不可能で、 そうすると感染が持続して流行が 定着するエンデミック (endemic)の状態が継続するものとして、感染の制御システムを構築する必要があります。
例えば、日本全体で1日の感染者数が100人程度で、感染を制御する場合どのようなシステムが必要でしょうか。
まず、規模感について考えてみますと、1日100人の感染の場合、感染が季節性をもたないものとしますと、1年間の感染者数は36,500人です。このとき、重傷者2割とすれば7,300人、死亡者を5%とすれば1,825人です。感染者を早期隔離するための必要検査数を陽性者率が1%とすると1日10,000件です。早期隔離以外に回復したかどうかなどの検査が5割程度必要と考えると、一日の検査機関の必要検査数は15,000件です。感染者の回復に要する期間が平均30日とすると、隔離施設の規模は2,400人、重傷者を収容する感染症病院の規模は600人程度です。もちろん稼働率を見越す必要はあります。
爆発的感染を防ぐためには、 実行再生産数\(R_e\) を常に、1以下にコントロール必要があります。
果たして、これは可能なのでしょうか?
上記したように、新型コロナウイルスの場合は、 R0 をドイツで推定している2.5とし、 感染期間の平均 τが30日程度としますと、βは0.083となります。そうすると実行再生産数 \(R_e\) を \(R_e<1\) にするには、 実行感染期間の平均 τ を τ <12にすればよいことになります。
したがって、理論的には感染者を平均12日以内に発見して隔離することができれば、制御可能となることとなります。
ここで、感染者とは病気をうつす可能性のある人で発症者ではありません。新型コロナウイルスの場合、厄介なことに無症状の感染者がいて、他の人に感染させますので、この人たちを含めて平均12日以内に隔離する必要があります。そのために追跡機関の働きが重要になります。
もし、隔離政策だけで、現在のロックダウンと同様にするには、 基本再生産数 R0 の8割削減ですから、 このときの実行再生産数 \(R_e\) 数は0.5で、 τ は6となり、 感染者を平均6日以内に発見して隔離する必要があることになります。
しかし、実際の世界ではこんなに単純ではありません。そこで、正確なデータによる予測システムが重要になります。予測システムにより、現時点の感染者数、 実行再生産数\(R_e\) を予想し、また将来の感染者数を予測し、追跡機関により、感染者を早期発見するのです。
そのためイメージは以下のようなものです。
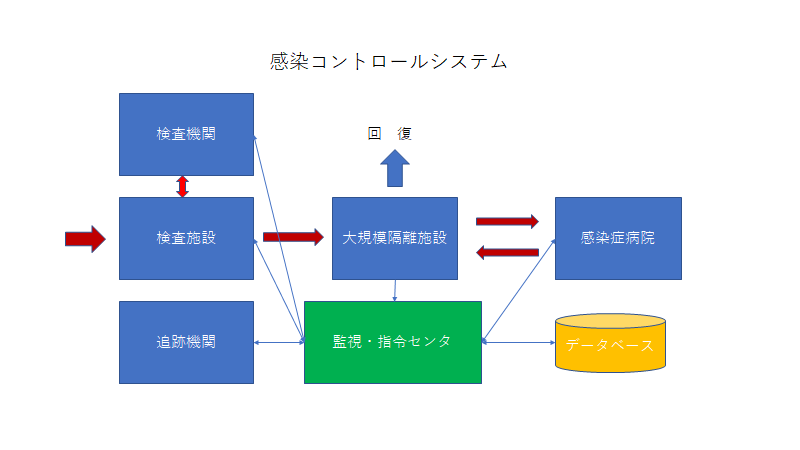
このシステムの目的
このシステムの目的は、感染者を早期に発見し隔離することにより、感染者数を定常化させ、感染者の早期治療による重傷者、死亡者を可能な限り減少させることです。
監視・指令センタ
監視・指令センタは感染に関する情報の一元化を行います。感染者や接触者の情報だけでなく、隔離施設、感染症病院などの施設の情報なども一括管理します。
感染者情報に基づき感染者数などをリアルタイムに予測し、見える化します。そして、 実行再生産数 \(R_e\) を1以下に制御します。
また、必要に応じて、サンプリング調査等を実施し、現状データの収集を行います。
これにより、追跡の強化など感染者を早期発見し、 関係機関に適切な指示をし、 実行再生産数 \(R_e\) を1以下に制御します。
検査施設
検査施設は全国に設け、台湾、韓国などが実施しているような効率的な検査体制をとることが望まれます。情報はすべて端末からセンタに送信します。
検査機関
検査機関は行政機関ではなく民間の検査機関を活用します。検査機関はセンタの指示により活動し、必要な情報をセンタに送信します。
追跡機関
追跡機関はセンタの指示により、実際に感染者や接触者の情報の聞き取り調査を行います。
感染する危険性があるので、訓練を受けた人が当たる必要があります。なので、できれば、追跡アプリなどの活用が望まれます。
大規模隔離施設
隔離施設は効率を考えると500人以上の収容できる施設がよいと思います。感染者間では感染しませんので、個室に隔離というよりは、娯楽施設が併設されているような楽しめるものにするのが効果的です。例えば、逆説的に、クルーズ船のようなもの
また、医師や看護師、従業者は免疫抗体がある人が望ましい。
感染病院
症状の重い人を受け入れ、軽くなると隔離施設に移転させます。 なお、医師や看護師、従業者は免疫抗体がある人が望ましい。
このブログの誤りや、ご意見のある方は、patent-konishi@kcn.jpまでご連絡ください。
