前回は、日本の新型コロナウイルス対策の戦略について、感染症の基本的な戦略である感染者の早期隔離が抜け落ちていること、簡単な感染症数理モデルにより早期隔離すれば、実行再生産数\(R_e\)を低減できることを指摘しました。

そして、緊急事態宣言の出口戦略として、二度とこのような事態に陥ることにならないように、 実行再生産数\(R_e\) を制御するための全体的なシステムのイメージを提案しました。

今回は、東京都とニューヨーク市の具体的なデータにより感染者数が今後どのように推移するのか、どのようにすれば感染をコントロールできるのか、をSIRモデルを使って数値計算しています。

感染の制御にとって最も重要な概念は前回のブログで指摘しましたように実行再生産数\(R_e\)です。 これを累計確認感染者数が何日で2倍になるかを示す倍加速度により、簡易的にもとめています。

この倍加速度が米国、イタリア、スペイン等の感染爆発が起こった国々と比較して、幸いにも、非常に緩やかであり、政府の感染対策の失敗にも拘わらず、日本では、欧米のような感染爆発が起きていないことを指摘しています。

そして、どのようにすれば東京都の感染の制御ができるか、その時、感染者はどのように推移するかを示しています。

また、これに基づいて、出口戦略として、今後どの程度の隔離政策をとれば、感染を制御できるかを計算しています。

なお、最近、入ってきたニューヨークの抗体検査、慶応大学病院の一般入院者に対する事前ＰＣＲ検査の結果を踏まえて、未確認感染者数が多い場合の新型コロナウイルス対策の戦略についても考察しています。

数式の苦手な方は数式を読み飛ばして考え方だけ追ってください。

日本の新型コロナウイルス感染状況の特異性

下図は、日本経済新聞が集計している全世界の感染者数の推移です。縦軸に確認感染者の累計数を対数表示で、横軸に確認感染者数が100人を超えてからの日数を表しています。

このグラフから日本の累計確認感染者数の動きが非常に特異なのが見て取れます。

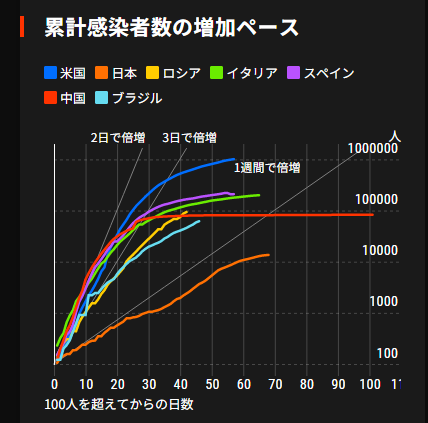
米国、イタリア、スペイン、イランなどは人口や人口密度に拘わらず、初期の累計確認感染者数が2倍になる倍加速度が2日から3日と急速に感染拡大していることが分かります。

一方、日本の累計確認感染者数が2倍になる速度は7日から10日です。

このグラフだけを見ていますと「ああそんなものか」ぐらいの感覚ですが、指数関数的増加は倍加速度により劇的に変化します。

この違いを見てみましょう。
前回、感染初期では、感染者数I(t)は
\[I(t) = I(0)\mathrm{e}^{ λ_0 t}\tag1\]
と表されると説明しました。Ｔ日間で、感染者数I(t)が2倍になるとすると\( λ_0 \)は
\[ λ_0 = \frac{ln2}{T}\tag 2\]
で表されます。
また、実行再生産数\(R_e\)とは次の関係式が成り立ちます。
\[R_e =1+ λ_0τ\tag 3\]
ここで、Τは感染者一人当たりの感染期間（人に移す可能性のある期間、したがって入院や隔離期間は含まない）を表します。

米国、イタリア、スペイン、イラン は倍加速度が3日から2日で実行再生産数 \(R_e\) が大きく累計確認感染者の増加は10日間で桁が1つずつ上がって行きます。爆発的増加です。

それに比べ日本の累計確認感染者数の増加速度は、倍加速度が10日から7日と他国に比べると緩やかです。

これは、非常に不思議です。そのため、他国から「日本は不当に検査数を抑えて確認される感染者数を少なく見せている。」といった批判がなされています。

次表は、倍加速度の違いにより、指数関数的増加はどのような様相を呈するかを示しています。

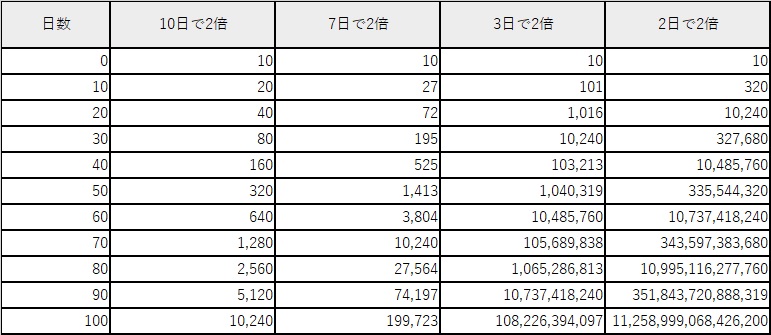
この批判は当たっているのでしょうか

日本は不当に検査数を抑えて確認される感染者数を少なく見せていないか

確かに、日本は検査数が異常に少ないので、確認されている感染者数が実際の感染者数と大幅な乖離があるのは否定できません。しかし、それにしては死亡者数がかなり低いし、これが非常に重要なことですが、死亡者数の倍加速度も10日から7日程度で、感染者数と同じように推移し、確認された感染者数に対する死亡率も他国にくらべ低くなっています。

下図は同じく日経新聞が発表している世界の死亡者の推移です。

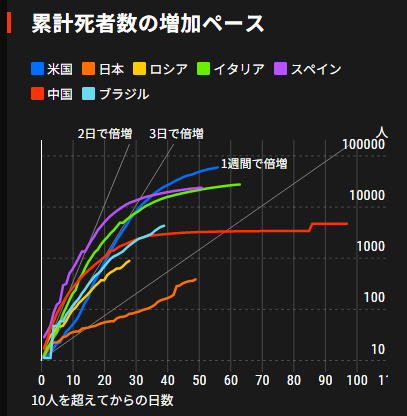
これは非常に重要なことですが、例え日本で未確認感染者が確認された感染者の100倍いたとしても、やはり倍加速度は7日程度であるということです。実行再生産数 \(R_e\) が変わらない限り、 米国、イタリア、スペイン、イラン のような爆発的な増加は起らないことになります。

なぜ日本では幸いなことに実行再生産数\(R_e\) が低く抑えられているのでしょうか

実行再生産数 \(R_e\) は(3)式で与えられるからΤに関係しますが、爆発的感染者が増加した 米国、イタリア、スペイン、イラン などでは、ロックダウンされるまでは、隔離政策が機能しなくて、感染期間Τはどの国もほぼ同じで新型コロナウイルスの感染能力のある期間にほぼ等しいと考えられます。Τが3週間程度としますと実行再生産数は倍加速度が分かれば自動的に算出されます。日本も検査が進まず隔離政策が機能していなかったとすると、米国等と同様にΤは3週間程度と考えてもほぼ間違いないでしょう。

実行再生産数 \(R_e\) はまた
\[R_e = β×Τ\tag 4\]
であ表されますから、日本の場合βが米国などに比べてかなり小さいと考えられます。Τは前回のブログで説明しましたように、1人が単位時間（1日）に感染させる割合ですが、これが小さいということは、ウイルスの感染力が変わらないものとすると、マスクなどによる防護、生活様式（靴を脱ぐなどの清潔さ等）、人との接触の仕方などの差によるものと考えられます。
すなわち、βは
\[β = f（ウイルスの感染力、人間同士の接触率、防護率、・・・・・）\]
といったものです。

したがって、世界各国で実施されてるロックダウン政策や日本の8割減は人間同士の接触率を小さくしてβを小さくする政策です。

日本では、新型コロナ対策の失敗にもかかわらず、日本の生活様式などで、神風のようにもともとβが小さく助けられてきているのは、非常に幸せなことです。

新型コロナ感染者数の東京とニューヨークの比較

もう少し、東京都とニューヨーク市について、実行再生産数 \(R_e\) の違いにより、どのように変わるのか検討します。

Fig.1は東京都において、倍加速度が10日に2倍とし、累計感染者数が2500に達したときに緊急事態宣言がなされて、実行再生産数が2.38から接触率を8割削減して、実行再生産数が0.477になる場合のSIRモデルによる数値計算例です。（推計値ではありません。）緑が新規感染者数、青が累計確認感染者数、赤が現在の確認感染者数（隔離、入院、死亡を除いたもの）です。

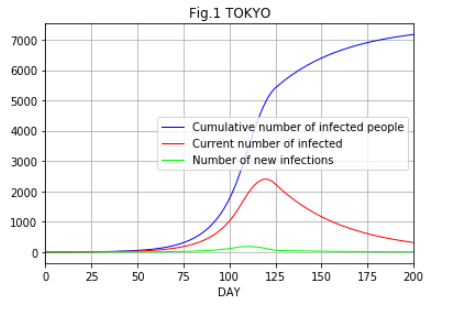
Fig.1では新規確認感染者数が分かりにくいので、Fig.2に新規確認感染者数のみを示しました。緊急事態宣言が発出された105日から20日をかけて実行生産数 \(R_e\) が2.386から8割減の0.477に比例的に変わるものとしています。したがって、新規感染者はしばらく上昇し、そして下降します。

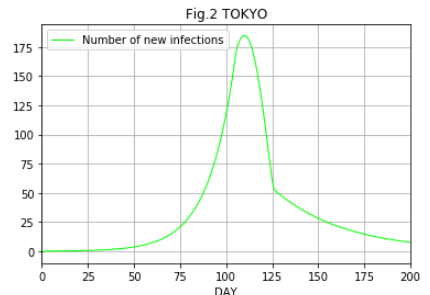
Fig.3は ニューヨーク市において、倍加速度が2日に2倍とし、累計感染者数が3000に達したときにロックダウンがなされて、実行再生産数が7.93から接触率を9割削減して、実行再生産数が0.793になる場合のSIRモデルによる数値計算例です。

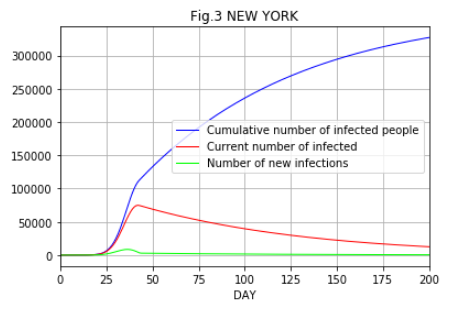
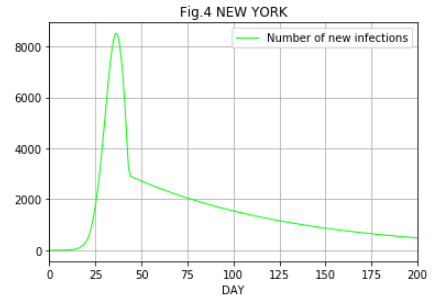
Fig.4は ロックダウンされた23日から20日をかけて実行生産数が7.93から9割減の0.793に比例的に変わるものとしています。 ニューヨーク市では東京都と違い政策実施前の実行生産数 \(R_e\) が大きので、ロックダウンをして接触率を9割減に削減しても、まだ、実行再生産数は0.793ですから減少速度が低くなっています。

いかに日本が恵まれた状況にあったのかが分かります。

出口戦略を考える

緊急事態宣言により、今後、日本の経済は劇的に悪化し、倒産会社が相当数に上るものと予想されます。したがって、早急に出口戦略を策定して、経済の立て直しを図る必要があります。

しかし、前回に提案しているような制御システムを組み込まないで、単に、経済活動を再開すると北海道のように再度感染者数が増加してしまいます。

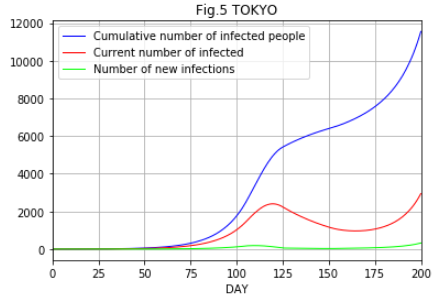
具体的に東京都の場合どのようになるか計算しますと下図のようになります。
これは、新規感染者数が30になる150日に20日かけて経済を再開した場合、1か月程度で100人まで増加し、それ以降指数関数的に増加することを示しています。

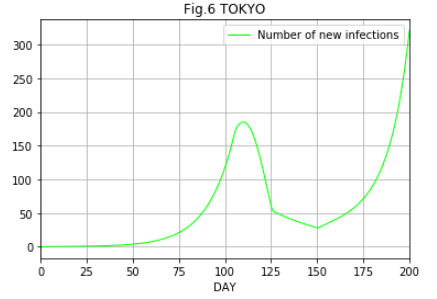
これを抑えるために、前回、提案している制御システムにより、感染者を早期に隔離して平均感染期間Τを小さくする必要があります。

東京都の場合は実行再生産数\(R_e\)を1より小さくするには、Τを8.39にすればよいことになります。

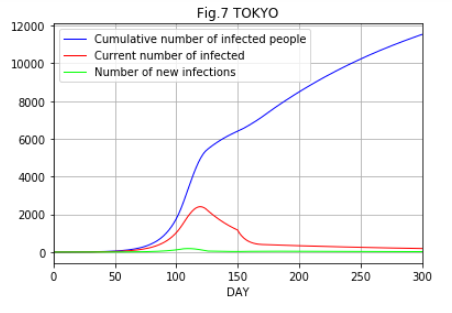
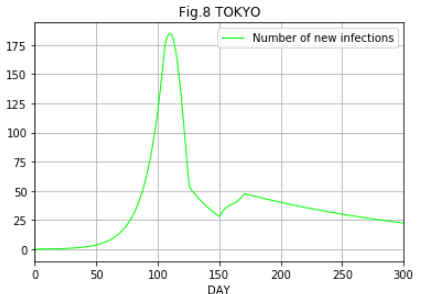
Fig.7、Fig.8にΤを8にした場合の図を示します。累積感染者数は増え続けますが、新規感染者数及び現在の感染者数は一定の数に抑えられることが分かります。

ニューヨーク市の場合は実行再生産数\(R_e\)を1より小さくするには、Τを2.52にする必要があり、制御が難しくなります。従って、これを実現するほど、平均のΤを小さくするには、経路追跡システムで濃厚接触者など、発症する前の人についても隔離するなどの対策も必要になります。

ニューヨークの抗体検査や慶応病院のPCR検査について

日経新聞によりますと「 米ニューヨーク州のクオモ知事は27日の記者会見で、新型コロナウイルスの抗体検査を7500人に増やした結果、14.9%で抗体が確認されたと発表した。3000人を対象とした22日時点の13.9%から1ポイント上昇した 」「 州内で最も感染者が多いニューヨーク市内では22日の21.2%から24.7%まで高まった。 」として、ニューヨーク市では250万人近く感染したことになり、公表値の10倍にあたるということです。抗体検査は本当に新型コロナウイルスだけを陽性と判定しているのか、通常の風邪コロナウイルスにも反応して陽性になっているのではないのかとの疑問もありますが、ありえない数ではないでしょう。

また、日本では慶応「 慶応義塾大学病院（東京都新宿区）は4月23日までに、新型コロナウイルス感染症以外の治療目的で来院した無症状の患者67人にPCR検査を行ったところ、4人（5.97％）が陽性者だったと公表した。4月13日から4月19日に行った術前および入院前PCR検査で明らかになったもの。 」としています。

これによりますと、母集団は小さいものの東京都は60万人が感染していることになり、感染確認者数4000人の150倍になります。ニューヨーク市の200万人は抗体検査によるものですので、すでに感染力をもたない人もいますので、現在の感染者数は東京都と同程度である可能性もあります。

たとえ、東京都の感染者数が150倍であったとしても倍加速度である実行再生産数 \(R_e\ に影響しませんので、今までの議論に影響しません。
なぜなら、
\[\frac{2×感染確認者数（4000） } {感染確認者数（4000） } = \frac{ 2×感染者数（60万） }{ 感染者数（60万） }\]

となるからです。

感染者数が60万人は少し多いようですけれども、すでに感染して回復している人が数倍いるわけですから、感染者に対するする東京都の死亡率は\(\frac{120}{600000}\)で0.02％でインフルエンザの0.1％よりもかなり低いことになり、これからの戦略を大きく変えることも可能になります。

したがって、本来感染状況を把握するために無作為抽出によるサンプリング調査を実施して実態把握すべきです。

実態把握なくして対策は打てませんし、正しい判断はできません。